
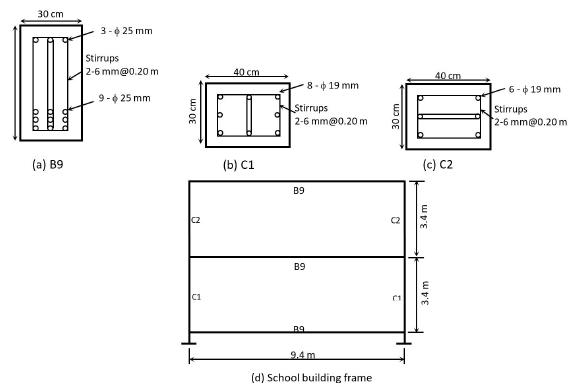

Īnother development took place within the statistical physics community, where the study of complex problems gave rise to other approaches such as the central-force elastic spring model, the random fuse model, and the elastic beam lattice. Although this system behaves like a granular material without cohesion, bonding was later introduced betwee the elements and the elements themselves have also been generalized to deformable polyhedral blocks. This simulated the mechanical behavior of unbonded disks and spheres of variable sizes, the equations of motion being deduced from Newton's second law with elements interacting directly via contact forces. An alternative approach was introduced four decades ago, the distinct element method, which is particularly well suited to describe granular media. Such features cannot be included in a satisfactory way in a continuum model. Concrete is a typical and commonly occurring example. Examples are granular, fibrous or porous materials where multiscale discontinuous features have a profound influence on the fracturing behavior. Many real materials, however, cannot be adequately described as a continuum.
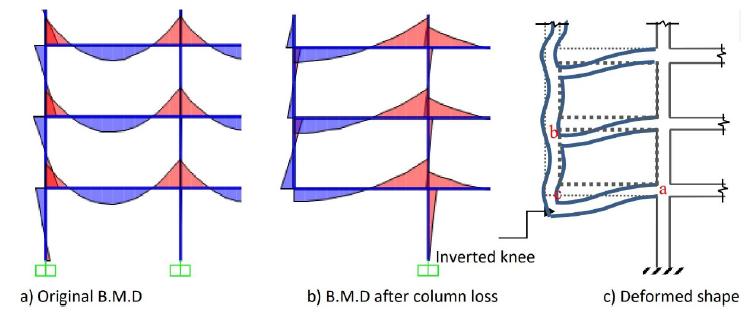
Material properties have long been studied by regarding the material as a continuum, such as in finite element analysis. It is proposed that the small-scale exponent ζ = 0.8 appears as a consequence of cleavage between crystal planes and consequently requires a different fracture criterion than that which is used on larger scales. In the present calculations we obtain ζ = 0.52, a value which remains constant for all disorders.
Sp column 4 81 cracked crack#
In the tensile case, the exponent which characterizes scaling of crack roughness with system size is found to be very close to the experimental value ζ ~ 0.5 when realistic fracture criteria are used. We consider two types of external loading, torsion applied to a circular cylinder and tension applied to a cube. Our results show that the inclusion of shear forces have a profound effect on crack morphology. Moreover the combination of bending and tension used in the old criterion is correct only for plastic deformations. The conventional choice has been to consider the combined loading as an interaction between bending and tensile forces only, leaving out shear forces altogether. Results are obtained with two criteria which are consistent with the theory of elasticity and compared with previous results using the original criterion, chosen when the method was first published. We study the effects realistic fracture criteria have on crack morphology obtained in numerical simulations with a stochastic discrete element method. Porelab, Department of Physics, Norwegian University of Science and Technology, Trondheim, Norway.


 0 kommentar(er)
0 kommentar(er)
